1. Definición y estructura de una matriz.
Podemos definir una matriz como un conjunto de números reales ordenados en filas (i) y columnas (j). La cantidad de filas y columnas que contenga la matriz nos indicará su dimensión. Así pues, una matriz de m filas y n columnas será una matriz de dimensión m x n.
Todas las matrices se representan a través de una letra mayúscula. Por ejemplo, la siguiente matriz…
… Es la matriz A de dimensión 4 x 3, porque tiene 4 filas y 3 columnas.
Los números incluidos dentro de una matriz se llaman elementos y estarán contenidos entre dos paréntesis ( ) o dos corchetes [ ]. Los elementos se designarán con la misma letra que hemos utilizado para nombrar la matriz, pero en minúscula, y acompañada por dos subíndices (i, j) que nos indicarán el cruce entre la fila (i) y la columna (j).
Así pues, en la matriz anterior, el número marcado….
… es el elemento a32, porque está en la tercera fila y segunda columna. Siempre se indicará primero la fila y después la columna.
2. Clasificación de las matrices.
Vamos a ver algunos tipos de matrices:
a) Vector fila: Son aquellas matrices que están formadas únicamente por 1 fila y n columnas.
La matriz C es un vector fila, porque está formada por 1 fila y 5 columnas. La designamos de la siguiente manera para indicar su dimensión C1x5.
b) Vector columna: Son aquellas matrices que están formadas únicamente por 1 columna y m filas.
La matriz D4x1 es un vector columna, porque está formado por 1 columna y 4 filas.
c) Matriz cuadrada: Es aquella matriz que tiene el mismo número de filas que de columnas, es decir m = n.
La matriz F3x3 es una matriz cuadrada porque tiene 3 filas y 3 columnas. Se dice que es una matriz cuadrada de orden 3.
Cabe destacar que el conjunto de los elementos donde i = j (es decir la fila y la columna son iguales) forman la diagonal principal. En F la diagonal principal la forman los elementos f11, f22 y f33.
Por otro lado, el conjunto de elementos donde i + j = orden + 1, forman la diagonal secundaria. La matriz F es de orden 3, por lo tanto todos los elementos donde i + j = 3 + 1, (i + j = 4) formarán la diagonal secundaria. Esto se cumple para los elementos f13, f22 y f31.
d) Dos matrices son iguales si tienen la misma dimensión y además coinciden término a término.
En este caso podemos decir que A = B ya que ambas son de dimensión 2 x 3 y se cumple que aij = bij
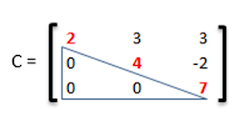
e) Matriz triangular superior: Es aquella matriz cuadrada en la que los elementos situados por debajo de la diagonal principal son nulos.
f) Matriz triangular inferior: Es aquella matriz cuadrada en la que los elementos situados por encima de la diagonal principal son nulos.
g) Matriz diagonal: Es aquella matriz cuadrada en la que todos los elementos que no están en la diagonal principal son nulos.
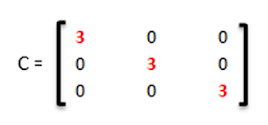
h) Matriz escalar: Es aquella matriz diagonal en la que todos los elementos de la diagonal principal son iguales.
i) Matriz identidad: Es aquella matriz escalar en la que todos los elementos de la diagonal principal son iguales a 1. Esta matriz se representa con la letra I y se puede añadir el subíndice, si es necesario, indicando su orden.
j) Matriz Nula: Es aquella matriz en la que todos sus elementos son iguales a cero.
k) Matriz transpuesta: La matriz transpuesta At de la matriz A es aquella que se obtiene al cambiar en A las filas por columnas y viceversa. Se puede indicar de la manera At o A’.
l) Matriz simétrica: Una matriz A es simétrica si se cumple que A = At . Como es de suponer, para que una matriz sea simétrica deberá ser necesariamente cuadrada.
La suma de dos
matrices, A y B de dimensiones m x n, da como resultado una nueva matriz, A+B, de igual dimensión m x n,
cuyos elementos son la suma de los términos que ocupan la misma posición en las
matrices A y B: (aij)m,n + (bij)m,n = (aij
+ bij)m,n
Pulsa aquí para acceder al video explicativo en Youtube
La
multiplicación de una matriz A por
un escalar o número k da como resultado una
nueva matriz, de igual dimensión que A, cuyos elementos son el producto de cada elemento de A por k:
k · (aij)m,n = (k · aij)m,n
Pulsa aquí para acceder al video explicativo en Youtube
3.3 Producto de matrices.
La multiplicación de dos matrices, A · B, puede realizarse si los vectores fila
de A tienen la misma cantidad de elementos que los vectores columna de B. Para
expresarlo de una forma más sencilla, diremos que dos matrices pueden
multiplicarse si el número de columnas de la primera es igual al número de
filas de la segunda.
Amxn · Bpxq ; es posible solo si n = p.
Ejemplo:
A5x3 · B3x2 : La multiplicación es posible, ya que el nº de columnas de A es 3 y el de filas de B también es 3.
A2x4 · B3x2 : La multiplicación no es posible, ya que el nº de columnas de A es 4 y el de filas de B es 3.
La matriz resultante de un producto de matrices tendrá como dimensión el nº de filas de la primera y el de columnas de la segunda. En el ejemplo anterior:
A5x3 · B3x2 : La matriz producto A · B tendrá 5 filas y 2 columnas: (A · B)5x2
El producto de dos
matrices A · B es otra matriz C cuyos elementos se obtienen multiplicando cada
vector fila de A por cada uno de los vectores columna de B, de tal manera que se
multiplicarán los elementos que tengan la misma posición en dichos vectores término
a término y se sumarán los resultados. El valor final obtenido en cada una de las operaciones ocupará la
posición: vector fila de A, vector columna de B en la matriz producto:
A = (aij) m,n ; B = (bjk) n,p
; A · B = C = (cik) m,p
Podemos efectuar las operaciones en el orden que queramos, siempre que coloquemos el resultado en la posición correcta de la matriz producto.
En el siguiente ejemplo realizaremos las operaciones en el siguiente orden:
vector fila 1 de A x Vector columna 1 de B = Término 1, 1 de C
vector fila 2 de A x Vector columna 1 de B = Término 2, 1 de C
vector fila 1 de A x Vector columna 2 de B = Término 1, 2 de C
vector fila 2 de A x Vector columna 2 de B = Término 2, 2 de C
vector fila 1 de A x Vector columna 3 de B = Término 1, 3 de C
vector fila 2 de A x Vector columna 3 de B = Término 2, 3 de C
... y de la siguiente manera...
Ejemplo 1: Supongamos las dos matrices A y B
A · B: Primero vamos a ver si se pueden multiplicar y cuál será la dimensión de la matriz producto.
Como vemos, la multiplicación de A · B es posible, y el resultado será una matriz de dimensiones 1 x 1, o sea, de un único término. Esto es así porque multiplicamos cada fila de A por cada columna de B y como solo hay una fila en A y una columna en B, el resultado es un solo término.
B · A: Primero vamos a ver si se pueden multiplicar y cuál será la dimensión de la matriz producto.
Como vemos, la multiplicación de B · A también es posible. Sin embargo, el resultado será una matriz de dimensiones 3 x 3. Esto es así porque multiplicamos cada fila de B por cada columna de A y como solo hay 3 filas en B y 3 columnas en A, el resultado es una Matriz de 3 x 3.
4. Propiedades de las
operaciones con matrices.
4.1 Propiedades de la suma de matrices.
Asociativa: (A + B) + C = A + (B + C)
Conmutativa: A + B = B + A
Elemento
neutro: Am,n + 0m,n = Am,n ; siendo 0m,n una matriz donde todos sus elementos son ceros.
Matriz opuesta: Am,n + (– Am,n)
= 0m,n ; siendo A = (aij) y –A = (-aij)
aij
+ (-aij) = aij – aij = 0ij
Por ejemplo:
4.2 Propiedades del producto de escalares por matrices.
Asociativa: k · (p · A) = (k · p) · A
Distributiva: k · (A + B) = k · A + k · B
( k + p) · A = k · A + p · A
4.3 Propiedades del producto de matrices.
Asociativa: Am,n · (Bn,p · Cp,q) = (Am,n · Bn,p) · Cp,q
Distributiva: Am,n · (Bn,p + Cn,p) = Am,n · Bn,p + Am,n
· Cn,p = Dm,p + Fm,p
El producto de matrices, en general, no cumple la propiedad conmutativa.
Am,n · Bn,m
≠ Bn,m · Am,n
En este caso se confirma tal afirmación en el mismo enunciado ya que el producto de la expresión del primer miembro de la igualdad (Am,n · Bn,m ) nos daría una matriz de dimensiones m x m mientras que el producto de la expresión del segundo miembro (Bn,m · Am,n) nos daría como resultado una matriz de dimensiones n x n.
Aún así, las matrices cuadradas
tampoco cumplen dicha propiedad de manera general:
Am,m · Bm,m
≠ Bm,m · Am,m
Veamos un ejemplo:
Sean las matrices A y B,
comprobemos si cumplen la propiedad conmutativa:
Así pues, podemos ver que la propiedad conmutativa no es válida en el producto de las matrices A y B.
5. 5. Matrices cuadradas.
Las matrices cuadradas cumplen con las propiedades vistas hasta ahora en el producto de matrices. Además de todas ellas vamos a ver algunas otras:
Matriz unidad: La Matriz Identidad In, en un producto de matrices cuadradas, es lo que podemos llamar matriz unidad. Este caso es una excepción donde si se cumple la propiedad conmutativa ya que podemos asegurar que: Mn,n · In = In · Mn,n = Mn,n
Ejemplo:
Se cumple que A · I3
= I3 · A = A
Matriz Inversa: La Matriz cuadrada
inversa A-1 a otra matriz cuadrada A es aquella que al multiplicar A
· A-1 el producto resultado
es igual a la Matriz unidad (I).
An · An-1
= In
Ejemplo:
Podemos asegurar entonces que la Matriz B
es la Matriz Inversa de A (A-1) ya que al multiplicar ambas el resultado es la
Matriz unidad (I2).
Nota: ¡Ojo! No confundir la
Matriz Inversa A-1 con la Matriz Traspuesta At.
Vamos a multiplicar ahora B · A
Por lo que tenemos otra excepción donde se cumple la propiedad conmutativa en el producto de matrices ya que: Mn · Mn-1 = Mn-1
· Mn = In
La Matriz inversa cumple además las siguientes
propiedades:
6. Inversa de una matriz por sistema de ecuaciones.
Para hallar la matriz inversa A-1
de una matriz A, sustituiremos los términos de la matriz inversa por
incógnitas. Seguidamente igualaremos el producto de A · A-1 a la
matriz unidad. Por último extraeremos las expresiones resultantes del producto
de cada uno de los vectores de ambas matrices, A y A-1, y lo
igualaremos con el término de la matriz unidad correspondiente. Veamos cómo
hallaríamos la matriz inversa del ejemplo anterior:
7.7. Inversa de una matriz por sistema de Gauss-Jordan.
Para hallar la matriz inversa A-1 de una matriz A por el método de Gauss-Jordan convertiremos la matriz A en la matriz unidad In efectuando sobre ella las transformaciones que sean necesarias mediante una serie de operaciones en sus filas que también se aplicarán a la matriz unidad In. Las operaciones que podremos emplear serán las mismas que se utilizan para resolver sistemas de ecuaciones por el método de Gauss. Estas serán:
1) Permutar dos filas: Fx < > Fn
2) Sustituir la fila x (Fx) por el resultado de multiplicar o dividir todos sus elementos por un número diferente de 0: Fx = k · Fx
3) Sustituir la fila x (Fx) por un múltiplo de ella, más otra fila (Fn) multiplicada por un número k: Fx = Fx · n + Fn · k
En resumen, el procedimiento sería el siguiente:
Procedimiento 1: Matriz A -> Se aplica operación 1, 2 o 3 | In -> Se aplica la misma operación 1,2 o 3
Procedimiento x: Se aplica el procedimiento 1 hasta que la Matriz A se haya transformado en In
Fin: Cuando la matriz A se haya transformado en In, la matriz resultante de efectuar las mismas operaciones en In será la matriz inversa de A (A-1):
Veamos cómo hallaríamos la inversa del apartado anterior por este sistema…
Nuestra meta es conseguir que la matriz A se transforme en la matriz unidad. Enseguida nos damos cuenta que los términos de valor cero de A, están en la diagonal principal, cuando deberían estar en la diagonal secundaria para que se parezca más a I. ¿Cómo hacemos esta transformación? Exacto, aplicando la operación 1, es decir, la permutación de la fila 1 por la fila 2 en ambas matrices (A e I). Entendemos por permutar, cambiar la posición de una por otra, y lo hacemos en ambas matrices, tal como hemos explicado.
8. Matrices singulares o degeneradas
Hallar su inversa utilizando el sistema de ecuaciones y el de Gauss-Jordan
Empezamos por el sistema de ecuaciones:
Extremos las expresiones resultantes de aplicar el producto de matrices.
Sustituimos el valor de la incógnita a obtenida en la expresión 1) en las expresiones 4) y 7)
Llegamos a un punto
donde la ecuación no tiene solución, ya que para una misma expresión (2g-5d)
obtenemos dos resultados diferentes (-4 y -3), algo que es imposible.
Cuando esto ocurre es que estamos ante una matriz singular o degenerada, es decir, que no tiene inversa.
Vamos a intentar hallar la inversa de A a través del método Gauss-Jordan.
Lo primero que haremos es colocar una
matriz identidad de igual dimensión junto a la matriz A.
El procedimiento que emplearemos será el
siguiente: primero transformaremos los elementos de la matriz A situados por debajo de la diagonal
principal en ceros. Luego haremos lo mismo con los elementos situados por
encima de la diagonal principal y, por último, transformaremos los elementos de
la diagonal principal en unos.
Paso1:
Empezaremos transformando el término a31
= 3 en 0.
Para ello, a la Fila3 le restaremos la Fila1 multiplicada por 3: F3 = F3 – F1 · 3
Esto es así porque el primer término de la
Fila1 es un 1. Al multiplicarlo por 3 se transforma en un 3 (3 · 1 = 3) y si
luego se lo restamos a la Fila3, el primer término de la Fila3 será igual a 0
(3 – 3 = 0). Veamos la transformación…
F1 · 3 = (1 3 0 |
1 0
0) · 3 = (1 · 3 3 · 3 0
· 3 | 1 · 3 0 · 3 0
· 3) = (3
9 0 | 3 0 0)
F3 – (F1 · 3) = (3
4 2 | 0 0 1) –
(3 9 0 | 3
0 0) = (3 - 3 4 - 9 2 - 0 | 0 - 3 0 - 0 1 - 0) =
= (0 -5 2 | -3
0 1)
Hemos transformado la Fila3 en ambas matrices mediante operaciones y ahora la sustituimos
en las matrices iniciales.
Paso2:
Vamos a seguir con el término a21
= 4 para transformarlo en 0.
Para ello realizaremos la siguiente
operación F2
= F2 – F1 · 4
F2 = (4
7 2 | 0 1 0)
– (1 3
0 | 1 0 0) · 4
F2 = (4
7 2 | 0 1 0)
– (4 12
0 | 4 0 0)
F2 = (0 -5 2 | -4
1 0)
Y hemos trasformado la Fila2 tal como
queríamos. La sustituimos en las matrices:
Paso3:
Vamos a transformar el último término por
debajo de la diagonal principal en 0. En este caso es el término a32
= -5
Realizaremos la siguiente operación: F3 =
F3 – F2
F3 = (0
-5 2 | -3 0 1) –
(0 -5
2 | -4 1 0)
F3 = (0 – 0 -5 – (-5)
2 – 2 | -3 – (-4) 0 – 1 1 – 0)
F3 = (0 0 0 | 1
-1 1)
Sustituimos en las matrices
Y hemos transformado el término deseado en
0. Sin embargo nos damos cuenta de que en la primera matriz tenemos una fila
(la Fila3 en este caso) en la que todos sus términos son ceros. Cuando
esto ocurre estamos ante una matriz singular o degenerada.
Esto es así porque el término a33
también se ha transformado en un cero. Para cambiarlo a 1 (la diagonal
principal han de ser todos 1), deberemos realizar una operación de suma en la
tercera fila, lo que también modificaría los términos a31 y a32
que ya tenemos transformados en 0.
9. Rango de una matriz
Podemos definir el rango de una matriz como el número de filas o columnas (vectores) que son linealmente independientes, es decir, que no se puede establecer una combinación lineal entre ellas.
Sea la matriz A.
Una vez que lo hayamos conseguido, el rango
de la matriz será el número total de filas en las que alguno de sus términos sean
diferentes de cero, es decir, que sean diferentes a (0 0
0 0 0)
Lo
primero que haremos será permutar filas y columnas a nuestra conveniencia. Es
interesante que el primer término de la primera fila (a11) sea el
menor número de todos los de la primera columna. En este caso, vamos a permutar
la primera fila por la cuarta.
Paso 1: F1 ↔ F4
Paso 2: Vamos a transformar
los términos a21 = 1, a31 = 2 y a41 = 9 en
ceros. Para ello efectuaremos la siguiente permutación: C1 ↔ C4
Con ello hemos conseguido dos ceros en los
términos a21 y a41
Paso 3: F3 = F3 + F1
F3 = (-1 1 3
2 0) + (1 0
2 1 -1) = (-1+1 1+0
3+2 2+1 0+(-1)) = (0 1 5
3 -1)
Sustituimos la transformación de la fila 3 en la
matriz
Lo siguiente que haremos será transformar los términos a32 = 1 y a42 = 8 en ceros, siguiendo con el escalonado de la matriz. Para ello emplearemos el término superior de la matriz A a esos dos términos, es decir el término a22 = 2, ya que si seguimos utilizando la primera fila podríamos cambiar los ceros de la primera columna que ya hemos conseguido.
Paso 4:
F3 = F3 · 2 – F2. Con esto conseguimos
que a32 = 0; (1 · 2) – 2 = 2 – 2 = 0
F4 = F4 – F2 · 4. Con esto conseguimos
que a42 = 0; 8 – (2 · 4) = 8 – 8 = 0
F3 = F3 · 2 – F2 = (0 1 5
3 -1) · 2 – (0 2
-1 1 2) = (0
2 10 6 -2) –
(0 2
-1 1 2)
F3 = (0 0
11 5 -4)
F4 = F4 – F2 · 4 = (0 8 7 9 4) –
(0 2
-1 1 2) · 4 = (0
8 7 9 4) –
(0 8
-4 4 8)
F4 = (0 0
11 5 -4)
Sustituimos las transformaciones efectuadas en la fila 3 y la fila 4
Paso5: Por último trasformamos el término a43 en 0.
F4 = F4 – F3 = (0 0
11 5 -4) – (0 0
11 5 -4) = (0
0 0 0 0)
Sustituimos en la matriz…
… y ya tenemos la matriz escalonada tal como queríamos
Comprobamos que tenemos una fila completa
de ceros, por lo que las filas linealmente independientes son tres y por lo
tanto podemos afirmar que Ran (A) = 3.
10. Ejercicios propuestos.
1) 1) Dada las matrices A y B,
calcula A2 + B2 + 2AB
Solución:
Vamos a marcar en
diferentes colores las operaciones que realizaremos.

Vamos a comprobar que se cumple la
propiedad asociativa en el producto 2AB (marcado en verde).
Hemos ejecutado el producto en el
siguiente orden 2 · (A · B). Es decir, hemos multiplicado primero A · B y el
resultado obtenido luego ha sido multiplicado por 2. El producto obtenido ha
sido:

2) Dada la matriz A prueba que se verifica A3 + I = 0 y usa esta igualdad para obtener A10.
Vamos a hallar primero A3
teniendo en cuenta que A3 = A2+1 = A2 · A1
= A2 · A
Primero calculamos A2
Ahora hallamos A3
Ahora comprobamos que A3
+ I = 0 (siendo I de orden 3, o sea I3)
Vamos a calcular ahora A10
Para ello tenemos en cuenta que...
Y sustituyendo A3 por –I en la
primera expresión tenemos que…
Sabemos que I es la matriz unidad y
podemos afirmar que –I = (-1) · I
Tenemos en cuenta que I es la matriz
unidad y sabemos que la unidad elevada a cualquier potencia siempre es la
unidad, por lo tanto:
También sabemos que cualquier matriz
multiplicada por la matriz unidad es igual a la misma matriz, o sea A · I = A,
por lo que...
3) Estudia el rango de la matriz siguiente y di el número de columnas que son linealmente independientes.
Vamos a utilizar el procedimiento de Gauss para hallar el rango de A, explicando cada operación efectuada.
Operación 1:
1) F2 = F2 – F1
F3 = F3 – F1
F4 = F4 – F1 · 3
F2 = F2 –F1 = (1
5 3 3) – (1
-3 -1 -1) = (0 8
4 4)
F3 = F3 –F1 = (1
1 1 1) – (1
-3 -1 -1) = (0 4
2 2)
F4 = F4 –F1 · 3 = (3 7
5 5) – (1 -3 -1 -1) · 3 = (3
7 5 5) – (3
-9 -3 -3) = (0 16
8 8)
Operación 2:
2) F3 ↔F2
Operación 3:
3) F3 = F3 – F2 · 2
F4 = F4 – F2 · 4
F3 = F3 – F2 · 2 = (0 8
4 4) – (0 4 2 2) · 2 = (0
8 4 4) – (0
8 4 4) = (0 0
0 0)
F4 = F4 – F2 · 4 = (0 16
8 8) – (0 4 2 2) · 4 = (0
16 8 8) – (0
16 8 8) = (0 0
0 0)
Hemos llegado al
escalonado de la matriz y tenemos dos filas con ceros, por lo que podemos
afirmar que Ran (A) = 2
¿Cuál será el número
de columnas linealmente independiente?
Por fuerza tiene que ser
dos también. Veamos la matriz A
¿Cuál sería la otra columna dependiente? Pues realmente podríamos escoger cualquiera de las tres, porque cada una de ellas se puede calcular con una combinación de las operaciones de Gauss efectuadas con las otras dos. Veámoslo.
C1 = C2 · (-1) +
C3 · 2
C2 = C1 · (-1) +
C3 · 2
C3 = (C1 / 2) +
(C2 / 2)
Quitamos C3 por ejemplo
Y nos quedan dos columnas linealmente independientes.
4) Estudia el rango de A
según el valor del parámetro m
Vamos a escalar la matriz para que a31 = 2, sea igual a 0.
Para ello efectuaremos la transformación: F3 = F3 + F1· 2
F3 = (2 0 m2 – 1) + (-1 0 1) · 2 = (2 0 m2 – 1) + (-2 0 2)
F3 = (0 0 m2 + 1)
Una vez escalada la matriz, observamos que si m = 0, F2 será linealmente dependiente al ser el vector (0 0 0), por lo que el rango de la matriz sería 2. Para el resto de valores el rango de la matriz será igual a 3, puesto que F3 nunca tendrá los valores (0 0 0) sea cual sea el valor de m.
Solución: Para m = 0; Ran(A) = 2
Para m ≠ 0; Ran(A) = 3












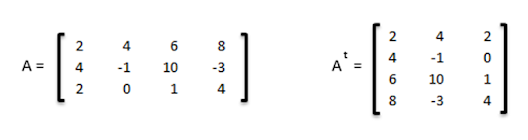














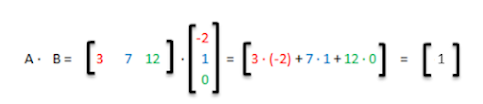






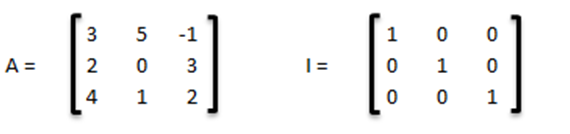













































































No hay comentarios:
Publicar un comentario