Proporcionalidad de segmentos. Semejanza.

1. Semejanza.

   Podemos decir que dos figuras son semejantes cuando ambas tienen la misma forma, aunque no por fuerza el mismo tamaño. Para que dos figuras sean semejantes deberán tener sus ángulos correspondientes iguales y las longitudes de sus segmentos correspondientes proporcionales. La razón de dicha proporcionalidad es lo que llamaremos razón de semejanza.

   Un ejemplo muy claro de semejanza lo podemos encontrar, por ejemplo, en la reproducción de un edificio mediante un plano a escala. La escala es el cociente entre la longitud de la reproducción y su correspondiente longitud en la realidad. Así pues, podemos considerar la escala como la razón de semejanza entre el plano y la realidad.

   

   En la imagen anterior tenemos el plano frontal de un rascacielos a una escala de 1 : 3.500, lo que quiere decir que cada unidad de medida en el dibujo corresponde a 3.500 unidades en la realidad. Como en el dibujo, el edificio mide 7 cm de altura, en la realidad medirá 7 cm x 3.500 = 24.500 cm, o sea 245 metros. 

   Podemos decir que el dibujo del edificio es semejante al real porque hay una razón de proporcionalidad evidente.

2. Proporcionalidad de segmentos. Teorema de Thales.

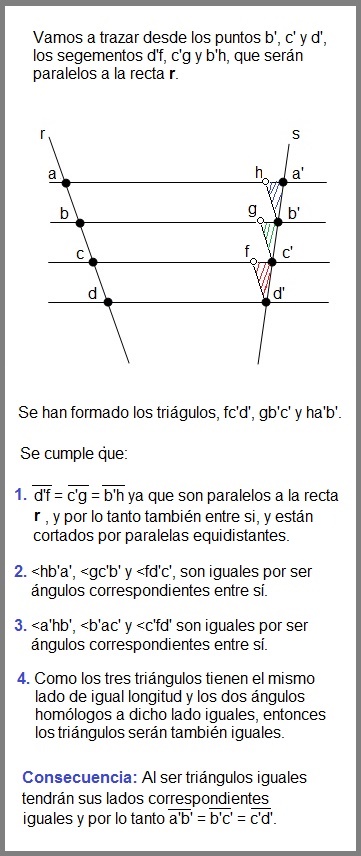
   Supongamos una recta r en la que hemos marcado cuatro puntos equidistantes, que llamaremos a, b, c y d. Seguidamente trazaremos una nueva recta, que llamaremos s, y cortaremos ambas con cuatro rectas paralelas entre sí, que pasarán por los puntos a, b, c y d. Los cuatro puntos de corte en la recta s serán los puntos a', b', c' y d'. 

      Vamos a demostrar que los segmentos a'b', b'c' y c'd', son iguales entre sí, lo que implicará que existe una razón de proporcionalidad con los segmentos ab, bc y cd respectivamente.

   Podemos, entonces, afirmar el teorema que dice: "Si varia paralelas determinan segmentos iguales en una transversal, también determinarán segmentos iguales en la otra transversal".

   Supongamos ahora, que tenemos varias paralelas, no equidistantes, que cortan a una recta r, y que también cortan a otra recta s.

   Podemos, entonces, afirmar el teorema que dice: "Si varias paralelas cortan a dos transversales, determinarán en ellas segmentos correspondientes proporcionales."

3. Semejanza de triángulos.

   Podemos decir que dos triángulos son semejantes cuando sus ángulos son iguales y sus lados homólogos son proporcionales. 

   En el ejemplo anterior los triángulos A y B son semejantes, pues sus tres ángulos miden lo mismo y sus lados homólogos son proporcionales (si un lado ha aumentado en una razón "x", los otros dos también han aumentado  en la misma razón). Vulgarmente diríamos que dos triángulos son semejantes sin son iguales en su forma aunque no en su tamaño. 

    Para que dos triángulos sean semejantes es suficiente que se den uno de los tres siguientes casos:

1. Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales. Esto es así porque todos sabemos que la suma de los tres ángulos de un triángulo es igual a 180º, por lo que el tercer ángulo tendrá que medir por fuerza lo mismo sin necesidad de comprobarlo.
2. Dos triángulos son semejantes si tienen un ángulo igual y los dos lados que lo constituyen son respectivamente proporcionales. 
3. Dos triángulos son semejantes si sus tres lados son respectivamente proporcionales.

   La semejanza de figuras cumple la siguientes propiedades:

1. propiedad reflexiva: Toda figura es semejante a sí misma.
2. Propiedad simétrica: Si una figura es semejante a otra, ésta última también es semejante a la primera.
3. Propiedad transitiva: Si una figura es semejante a otra y ésta segunda es semejante a una tercera, la primera también es semejante a la tercera.

   Al cumplir con las tres anteriores propiedades, podemos decir que la semejanza es una relación de equivalencia.

   Si los triángulos son rectángulos los casos de semejanza son más simples al tener en cuenta que uno de los ángulos será siempre de 90º

1. Dos triángulos rectángulos son semejantes si tienen un ángulo agudo igual.
2. Dos triángulos rectángulos son semejantes si sus dos catetos son proporcionales.
3. Dos triángulos rectángulos son iguales si uno de los catetos y la hipotenusa son proporcionales.

4. Ejercicios propuestos.

1) Los lados de un triángulo miden 3, 4 y 5 cm, respectivamente. ¿Cuánto medirán los de otro triángulo semejante de 18 cm de diámetro?

   Lo que observamos a primera vista es que para hallar la medida de los lados del triángulo resultante necesitamos saber la razón de semejanza entre ambos. 

  Si existe una razón de semejanza entre ambos triángulos, también la existirá entre la suma de sus lados, es decir, entre sus perímetros.

  Sabemos que el perímetro del triángulo resultado es 18 cm y que el perímetro del triangulo inicial sera la suma de sus lados, o sea Pi = 3 + 4 + 5 = 12 cm.

   La razón entre Pi y Pf será R = 18/12 = 3/2.

   Ahora aplicamos la razón a cada uno de los lados del triángulo y tendremos que..

    L1 = 3 x 3/2 = 4,5 cm.

    L2 = 4 x 3/2 = 6 cm.

    L3 = 5 X 3/2 = 7,5 cm.