Un sistema rectangular de ejes de coordenadas cartesianas, llamado así en honor a Descartes, está formado por dos líneas rectas perpendiculares entre sí, que se cortan en un punto formando cuatro ángulos rectos.
La línea recta horizontal XOX- es el eje de las x o eje de abscisas. La línea recta vertical YOY- es el eje de las y o eje de las ordenadas. El punto O donde se cruzan ambas, es lo que llamamos origen de las coordenadas y divide el eje de las abscisas en dos semiejes, positivo hacia su derecha y negativo hacia su izquierda, e igualmente en dos semiejes al eje de las ordenadas, positivo hacia arriba y negativo hacia abajo.
Cualquier punto representado dentro del sistema rectangular de ejes, vendrá definido por sus coordenadas cartesianas que están formadas por su abscisa (distancia del punto al eje de las ordenadas ) y por su ordenada (distancia del punto al eje de las abscisas).
La anotación empleada para indicar un punto es (x, y), donde x es la abscisa e y la ordenada.
Como podemos ver, el sistema queda dividido en cuatro secciones llamadas cuadrantes.
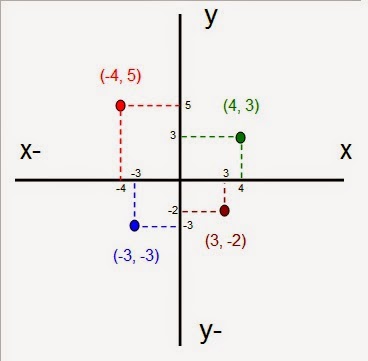
1 er cuadrante (+x, +y): Cualquier punto en este cuadrante es positivo para las x y las y.
2 º cuadrante (-x, +y): Cualquier punto en este cuadrante es negativo para las x y positivo para las y.
3 er cuadrante (-x, -y) : Cualquier punto de este cuadrante es negativo tanto para las x como para las y.
4 º cuadrante (+x, -y) : Cualquier punto en este cuadrante es positivo para las x y negativo para las y.
Veamos unos ejemplos.
Vamos a hallar, por ejemplo, el punto (4, 3): Contamos 4 unidades sobre el eje de las abscisas (x) en las unidades positivas (hacia la derecha) y trazamos una línea paralela al eje de las ordenadas (y). Seguidamente contamos 3 unidades sobre el eje de las ordenadas (y) en las unidades positivas (hacia arriba) y trazamos una línea paralela al eje de las abscisas (x). Donde se crucen ambas líneas obtendremos el punto (4, 3). Este punto se encuentra alejado del eje de las ordenadas 4 unidades y del eje de las abscisas 3 unidades.
La abscisa del punto será AB = OC = 4 y la ordenada CB = OA = 3. Sus coordenadas serán AB = 4 y CB = 3. (4, 3).
Nota: Como vemos en este ejemplo, el papel cuadriculado es perfecto para la representación gráfica de puntos en un plano cartesiano.
Por lo que hemos explicado podemos observar que:
- Las coordenadas del punto de origen son (0, 0)
- La abscisa de cualquier punto situado sobre el eje de las ordenadas es 0; (0, n).
- La ordenada de cualquier punto situado sobre el eje de las abscisas es 0; (n, 0).
Podemos definir una función y = f(x), como un criterio tal que a cada valor de la variable x corresponde uno o varios valores determinados de la variable y. No vamos a entrar en detalle dentro del tema de las funciones debido a su extensión, sino que nos ceñiremos a su representación gráfica.
A través de la función y = f(x), tomaremos los diferentes valores de x como abscisas, y sus valores correspondientes de y como ordenadas. De esta manera conseguiremos una serie de puntos en el plano con los que, mediante su interpolación, realizaremos el gráfico de la función.
Veamos los diferentes gráficos que podemos obtener, dependiendo del tipo de función o ecuación aplicada.
3. Representación gráfica de una función lineal de primer grado.
Sea la función lineal de primer grado: y = 3x.
Vamos a dar diferentes valores a x para hallar su correspondencia en y.
x = -2 ; y = -6
x = 0 ; y = 0 Vamos a representarla gráficamente.x = 3 ; y = 9
Observamos que la recta de la función pasa por el origen de las coordenadas (0, 0). Esto es debido a que en este tipo de funciones en la que no existe término independiente, cuando la abscisa vale 0, la ordenada siempre valdrá 0.
Veamos ahora la función y = 2x + 3
x = -3 ; y = -3
x = 0 ; y = 3 x = 2 ; y = 7
En este caso la recta de la función no pasa por el origen de las coordenadas, sino que corta el eje de las ordenadas por el punto A (+3) y el eje de las abscisas por el punto B (-1,5). El punto A se obtiene cuando x = 0 y el punto B cuando y = 0.
y = 2 · (0) + 3 = 0 + 3 = 3 ; Coordenada (0, 3)
0 = 2x + 3
-2x = 3
2x = -3
x = -3/2 = -1,5 ; Coordenada (-1,5 , 0).
'OA' es el intercepto sobre el eje de las ordenadas (3), y 'OB' es el intercepto sobre el eje de las abscisas (-1,5). En este tipo de funciones el intercepto en el eje de las ordenadas es igual al término independiente (+3).
4. Representación gràfica de funciones de segundo grado.
Sea la función:
Demos varios valores a x.
Una vez interpolamos los puntos obtenidos a través de la función, vemos que la gráfica representa una parábola ilimitada. Al tratarse de una línea curva, el resultado será más preciso cuanto más puntos intermedios extraigamos de la función.
Como x esta elevado al cuadrado tanto si su valor es positivo o negativo, el resultado final para y será positivo e idéntico. Por ejemplo:
x = 2 ; y = 4
x = -2 ; y = 4
Esto provoca que se creen puntos simétricos respecto al eje de las ordenadas, lo que obliga a que la representación gráfica sea una parábola.
Veamos la función:
Veamos ahora la siguiente ecuación:
Despejando la incógnita x nos queda.
Veamos su gráfico.
Y obtenemos una elipse. Aquí hemos de tener en cuenta que se trata de una ecuación de segundo grado del tipo:
Para cualquier valor de y menor que -5 o mayor que 5 no existe la raíz cuadrada, pues el número contenido en el radical sería negativo y como ya sabemos no existe raíz cuadrada de un número negativo. Por otra parte al tratarse de un radical a cada valor de y corresponderán dos valores para x ,uno con signo positivo y otro con signo negativo.
Veamos el gráfico.
Como vemos el gráfico es un circulo cuyo centro esta situado en el origen de las coordenadas y cuyo radio es igual a la raíz cuadrada del término independiente de la ecuación.
Modifiquemos ahora un poco la ecuación y despejemos la x:
Demos valores a y para obtener los de x.
Y obtenemos una elipse. Aquí hemos de tener en cuenta que se trata de una ecuación de segundo grado del tipo:
Este tipo de ecuaciones está representada siempre por una elipse cuyos semiejes tiene como medida las raíces de los coeficientes de las incógnitas (2 y 6). Podemos comprobar que el término independiente, que es 144, corresponde al producto de los coeficientes de ambas incógnitas, es decir al producto de 2 al cuadrado y 6 al cuadrado. Cuando los dos coeficientes de las incógnitas son iguales la figura representada será, como podemos suponer, un círculo.



















No hay comentarios:
Publicar un comentario