Una ecuación de primer grado con dos incógnitas, es aquella que, como su nombre indica, posee dos incógnitas diferentes (normalmente x e y) que tienen como mayor exponente la unidad. Por ejemplo.
2x - 3y = 11
Una sola ecuación con dos incógnitas es indeterminada, pues el valor de cada incógnita dependerá del que tenga la otra, siendo así las posibles soluciones a ambas infinitas.
Dos o más ecuaciones de primer grado con dos o más incógnitas son simultaneas cuando, considerándolas de manera conjunta, se satisfacen para iguales valores de sus incógnitas. Según la cantidad de valores que puedan adoptar la incógnitas serán determinadas (un único valor común para cada incógnita) o indeterminadas (múltiples valores ilimitados comunes para cada incógnita). Por ejemplo.
2x - 3y = 11
x + y = 19
En este caso existe un valor común para cada incógnita que satisfacen las ecuaciones. Así x valdrá 10 e y valdrá 3 para ambas ecuaciones. Son ecuaciones determinadas.
Para que dos ecuaciones simultaneas tengan un único resultado común para cada una de sus incógnitas, deberán ser independientes y compatibles entre ellas.
Dos ecuaciones son independientes cuando no se obtienen una a partir de la otra, como en el ejemplo anterior. Si se obtienen una a partir de la otra se llaman equivalentes. Por ejemplo:
5x - 2y = 1
10x - 4y = 2
La segunda ecuación se obtiene multiplicando por 2 la primera. En este caso la segunda ecuación no nos aporta ningún dato nuevo, por lo que no podríamos encontrar una única solución para las incógnitas. Ambas ecuaciones son equivalentes y los valores para sus incógnitas son iguales e infinitos. Las ecuaciones equivalentes son indeterminadas.
Para que dos ecuaciones sean compatibles tienen que depender una de la otra, complementándose para tener una solución común para sus incógnitas. Si esto no es así, nos hallamos ante ecuaciones incompatibles. Por ejemplo:
3x + y = 10
6x + 2y = 2
En este caso son incompatibles porque como podemos ver es imposible que la igualdad de la segunda ecuación (2) sea menor que la de la primera (10) cuando el primer miembro de la segunda ecuación es el doble que el de la primera. En este caso el valor de las incógnitas no es coincidente, o sea, no existe una solución común.
La reunión de dos o más ecuaciones simultaneas con dos o más incógnitas es lo que llamamos sistema de ecuaciones.
Para resolver un sistema de ecuaciones, nos harán falta tantas ecuaciones simultaneas como incógnitas tengamos que determinar. En este capítulo nos ocuparemos de los sistemas de dos ecuaciones simultaneas compatibles e independientes de primer grado con dos incógnitas. (¡¡¡toma ya con el nombrecito!!!).
Veamos un esquema de lo explicado hasta ahora para entenderlo mejor:
2. Resolución de sistemas de ecuaciones.
Para resolver un sistema de ecuaciones de primer grado con dos incógnitas empleamos varios métodos de eliminación, que nos permiten transformar las dos ecuaciones en una única ecuación de primer grado con una incógnita.
Existen tres métodos de eliminación: Sustitución, igualación y reducción.
Nota: Existe también el método por determinantes que veremos en otro capítulo debido a su extensión.
a) Método de sustitución.
Este método consiste en despejar una incógnita de una de las dos ecuaciones y sustituirla en la otra. De esta manera conseguimos una única ecuación con una incógnita.
Ahora sustituiremos el valor de y calculado en cualquiera de las dos ecuaciones.
Así pues los valores para x e y que satisfacen las dos ecuaciones son 3 y 5 respectivamente. Vamos a sustituir dichos valores en ambas ecuaciones para comprobar la igualdad.
2x + 5y = 31 4x - 7y = -23
2 (3) + 5 (5) = 31 4 (3) - 7 (5) = -23
6 + 25 = 31 12 - 35 = -23
31 = 31 -23 = -23
Se llega en ambos casos a una identidad. Así pues los resultados para x e y son correctos.
b) Método de igualación.
Este método consiste en despejar la misma incógnita de ambas ecuaciones. Como el valor de las dos incógnitas ha de ser el mismo se igualan sus igualdades, lo que nos dejará una ecuación única de primer grado con una incógnita. Veámoslo con la misma ecuación del ejemplo anterior.
Hacemos el mismo procedimiento, pero esta vez despejando la incógnita y de ambas ecuaciones.
c) Método de reducción.
En este método se igualan los coeficientes de una de las incógnitas, multiplicando o dividiendo una de las ecuaciones por una cantidad, lo que, como sabemos, no modificará los valores de las incógnitas.
Al multiplicar por 2 la segunda ecuación por completo, lo que hacemos es crear una ecuación equivalente a la anterior. Así conseguimos igualar los coeficientes de las x.
Seguidamente restamos las dos ecuaciones porque lo que nos interesa es eliminar una de las incógnitas. en este caso la x.
Como sabemos, si sumamos o restamos una misma cantidad a los dos miembros de una ecuación, la igualdad subsiste y los valores de las incógnitas no varían. En este caso restamos al primer miembro de la primera ecuación la cantidad 4x + 10y y al segundo miembro le restamos 62 que son cantidades iguales (4x + 10y = 62).
El resultado nos deja una ecuación de primer grado con una incógnita. Vamos a resolverla.
-17y = -85
y = -85 / -17 = 5
Realicemos la misma operación pero igualando la incógnita y.
En este caso como los coeficientes de las incógnitas y son primos entre si (7 y 5), multiplicaremos cada uno de ellos por el coeficiente de la otra, consiguiendo así igualarlos. El coeficiente que se obtiene como resultado es el m.c.m de ambos (35). Seguidamente como vemos que ambos coeficientes tienen signos contrarios en vez de restar, sumaremos ambas ecuaciones.
El sistema de reducción es el más sencillo de los expuestos, pues nos lleva directamente a despejar la incógnita y nos evita muchas operaciones. Aún así, habrá gente que se encuentre más cómoda utilizando el de igualación o sustitución. Es criterio vuestro encontrar el que mejor os vaya y utilizarlo.
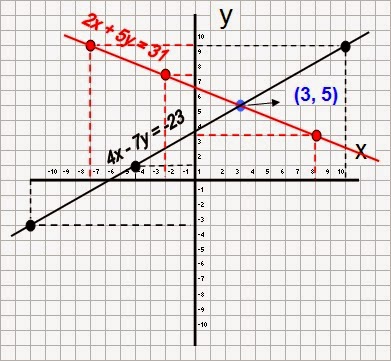
Vamos a representar gráficamente el sistema de ecuaciones que hemos utilizado hasta ahora como ejemplo.
4x - 7y = -23
2x + 5y = 31
Como sabemos cada ecuación por si sola representa una recta en un sistema rectangular de eje de coordenadas. Las coordenadas de cada punto de dichas rectas será una solución válida para las incógnitas x e y de cada ecuación. Esto es así porque cada ecuación del sistema, si la tomamos independientemente una de la otra, es indeterminada,es decir tiene infinitas soluciones para cada una de sus incógnitas ya que el valor de cada una de ellas va a depender del que le demos a la otra.
Lo que haremos primero será despejar la misma incógnita de cada ecuación. Por ejemplo la x.
Vamos a dar diferentes valores a la incógnita y de cada ecuación para hallar los correspondientes a la x.
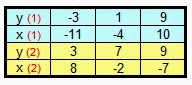
Ahora crearemos el gráfico correspondiente a las dos rectas que representan cada ecuación uniendo los puntos obtenidos que son:
4x - 7y = -23 (1) : (-11, -3) ; (-4, 1) ; (10, 9)
2x + 5y = 31 (2) : (8 , 3) ; (-2 ,7) ; (-7, 9)
Vemos que las rectas se cruzan en un punto (3, 5). Este punto será la solución común para las incógnitas de ambas ecuaciones, es decir la solución del sistema de ecuaciones, siendo x = 3 e y = 5.
Vamos a representar ahora el gráfico del sistema de ecuaciones equivalentes vistas en el apartado 1.
5x - 2y = 1 (1)
10x - 4y = 2 (2)
Despejamos la incógnita x.
Damos valores a la incógnita y obteniendo sus respectivos en x:
Como vemos para unos mismos valores de y obtendremos idénticos valores de x, otra prueba más de la equivalencia de ambas ecuaciones. ¿y como será el gráfico del sistema?.
coordenadas (1): (-1,-3) ; (1, 2) ; (3, 7)
coordenadas (2): (-1,-3) ; (1, 2) ; (3, 7)
¡¡¡ Exacto !!! , se sobrepondrán una recta sobre la otra, porque los valores de sus incógnitas siempre serán los mismos. A diferencia de los sistemas de ecuaciones independientes cuya representación gráfica de sus rectas se cruzan en un punto que es la solución común de sus incógnitas, las ecuaciones equivalentes sobreponen sus rectas una sobre otra por lo que su solución son todos los puntos que conforman las rectas (solución ilimitada).
Veamos por último el gráfico de las dos ecuaciones incompatibles del apartado 1.
3x + y = 10 (1)
6x + 2y = 2 (2)
Despejamos las x.
Damos valores a y para hallar las x.
Obtenemos las coordenadas.
(1) : (5, -5) ; (3, 1) ; (1, 7)
(2) : (2, -5) ; (1,-2) ; (-1,4)
Realizamos el gráfico.
Como observamos las rectas de ambas ecuaciones son paralelas entre sí, por lo que no se cruzarán en ningún punto, es decir, no hay una solución común para ambas ecuaciones.
No hay comentarios:
Publicar un comentario